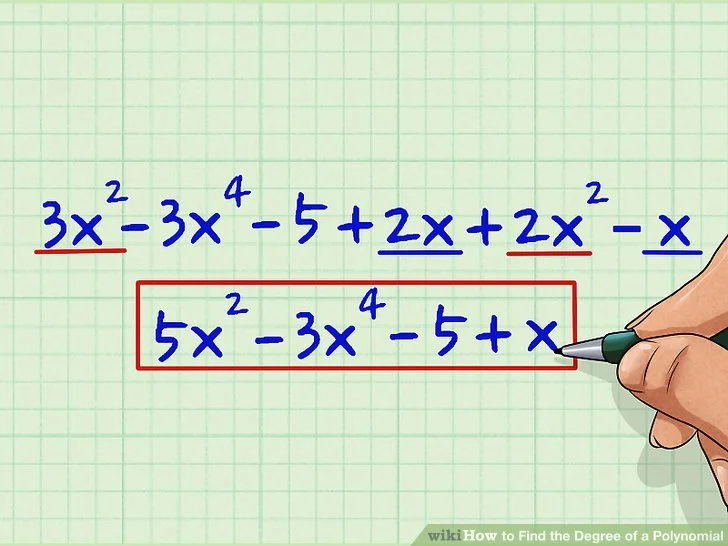Polynomial equations mean the relation between numbers and variables are explained in a pattern.
Table of Contents
What is a Polynomial?
Polynomial is an algebraic expression, in which the variables have non-negative powers. A polynomial function is an equation, which consists of a single independent variable, where the variable can occur in the equation more than one time with different degrees of the exponent. A polynomial expression is the one, which has more than two algebraic terms. As the name suggests, Polynomial is a repetitive addition of a monomial or a binomial.
Types of Polynomial
Polynomial equation is of four types :
- Monomial: It may be define as the polynomial which contains only one term. For example, x2 , x, y,v, 2y, 5z etc.
- Binomial: The polynomial which contains only two terms is called Binomial. For example, x2 – 12x
- Trinomial: The polynomial which contains three terms. For example, x2 – 11x+12
- Quadratic Polynomial: It is type of polynomial which contains four terms. For example, x3+23x2 – 15x-12
The general Polynomial Formula is,
F(x) = anxn + bxn-1 + an-2xn-2 + …….. + rx +s
- If n is a natural number: an – bn = (a – b)(an-1 + an-2b +…+ bn-2a + bn-1)
- If n is even (n = 2a): xn + yn = (x + y)(xn-1 – xn-2y +…+ yn-2x – yn-1)
- If n is odd number: xn + yn = (x + y)(xn-1 – xn-2y +…- yn-2x + yn-1)
Type of Polynomials
- Linear Polynomials: ax + b = 0
- Quadratic Polynomials: ax^2 + bx + c = 0
- Cubic Polynomials: ax^3 + bx^2 + cx + d = 0
Polynomial Identities
- (x + y)2= x2 + 2xy + y2
- (x – y)2= x2 – 2xy + y2
- x2– y2 = (x + y)(x – y)
- (x + a)(x + b) = x2+ (a + b)x + ab
- (x + y + z)2= x2 + y2 + c2 + 2xy + 2yz + 2zx
- (x + y)3= x3 + y3 + 3xy (x + y)
- (x – y)3= x3 – y3 – 3xy (x – y)
- x3+ y3 = (x + y)(x2 – xy + y2)
- x3– y3 = (x – y)(x2 + xy + y2)
- x3+ y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
- ax2 + bx + c = 0 then x = \frac{( -b \pm \sqrt{(b2 – 4ac)} )}{2a}